碁というゲームのゲームバランスはかなり微妙に保たれているように思えて,面白い。たとえばD16に隅の星に白石が置いてあるとする。このとき黒はC17に入って活きを得ることができる。ゲームバランスとなると単に活きを得るだけで有利になったとは断言できないで,代わりに白は中央が厚くなる。厚みは布石を築く上で重要な要因になるので,黒はC17に踏み込むタイミングが肝心になる。シンプルなルールにしてこの手順がちゃんとあるというのはほんと奇蹟的なんじゃねえの。
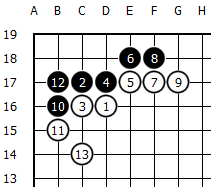
↑2から黒が飛び込み,13までで一段落。黒活き。
突飛な考えだが,碁盤が3次元であったら碁というゲームは成立しづらそうである。整数座標三つで打点を表すとすると,(i,j,k)の石を取るのに(i±1, j±1, k±1)(複合任意)の2^3=8箇所に石を置かねばならない。逆に,味方の石をつなぐのであれば八方からつなげるのであり,逃げることは容易である。一つ石を棒状につなぐだけで呼吸点が4つ増えるようでは,逃げるのが簡単すぎるかもしれない。
しかしそれは相手にとっても同様であり,相手の眼形の内部で活きを得るのもまた容易ということに違いない。終局図は蛇のように細長い石が絡み合うことになるかもしれない。それこそ無数の複雑な変化が現れる。考えてみれば3D囲碁がゲームバランス的にどうなるかというのは単純ではなさそうである。ゲームバランスという量を適当に定量する方法があれば,計算科学にとって面白いんじゃないかと妄想してみる。面白いと言われるゲームは問題の計算量クラスに特徴があったりするんかねえ?